Вещественные числа

Формат представления числа

Для хранения и обработки вещественных чисел большинство процессоров используют формат IEEE 754. Есть удобный калькулятор. Рассмотрим, как устроен формат, на примере 32-битных вещественных чисел:

Float example

Биты числа разделены на 3 группы:

  1. Знаковый бит. Один, старший бит. 0 – число положительное (или нуль), 1 – отрицательное или нуль.
  2. Показатель степени. 8-битное целое число, занимает биты с 23-го по 30-ый. Означает степень двойки, на которую будет домножаться основаная часть числа, записанная далее.
  3. Дробная часть. 23-битное целое число, содержащее значащие биты вещественного числа.

Обозначим знаковый бит как sign, беззнаковое значение показателя степени как exp, а беззнаковое значение дробной части как frac.

Значение числа в разных случаях

Итак, как числа получаются с помощью этих компонент? Есть несколько случаев:

  • Если \( 0 < exp < 255 \), число называется нормализованным. В таком случае оно равно \( -1^{sign} × 2^{exp - 127} × 1,frac_2 \), то есть знак и степень двойки домножаются на число, у которого в целой части стоит 1, а двоичную дробную часть составляют 23 бита frac.

Т. к. мы хотим представлять как большие по модулю числа, так и близкие к нулю, то степень двойки должна принимать как положительные, так и отрицательные значения. Поэтому мы вычитаем из неё 127 (смещение), так степень станет принимать значения [-126; 127] (почему не могут быть -127 и 128, увидим ниже).

Пример нормализованного числа

  • Если exp=0, число называется денормализованным. В этом случае его значение \( -1^{sign} × 2^{-126} × 0,frac \).

Пример денормализованного числа

  • Если exp=255 и frac=0, число называется бесконечностью и обозначается +inf или -inf в зависимости от знака.

Пример бесконечности

Бесконечности нужны для обозначения очень больших по модулю чисел, для представления которых не достаточно 8 бит показателя степени.

  • Если exp=255 и frac!=0, число называется нечислом и обозначается "NaN". Знак при этом ни на что не влияет.

Пример нечисла

Как видно, различных NaN-ов бывает много. Все они нужны для обозначения неопределённости в результате выполнения арифметических операций, например, inf-inf или sqrt(-3).

Итого, числовая прямая выглядит так: Визуализация числовой прямой

Особенности формата

  • Есть два нуля: +0 и -0. +0 имеет все нулевые биты, то есть является нулём как 32-битное целое число.

  • Сравнение: наименьшее положительное нормализованное число (\( 2^{-126} * 1,0\)) больше наибольшего денормализованного числа (\( 2^{-126} * 0,111..1\)). Также любое положительное нормализованное число с меньшим exp меньше любого положительного нормализованного числа с большим exp. Таким образом, действительно, все положительные денормализованные числа меньше всех положительных нормализованных, а нормализованные расположены в порядке показателя степени.

  • Такой же порядок остаётся, если сравнивать битовые представления вещественных чисел как знаковые целые числа! (Кроме NaN-ов).

  • Вещественные числа становятся более разреженными при увеличении их модуля. Чем число ближе к нулю, тем оно ближе к ближайшему к нему другому представимому числу. А точнее, денормализованные числа и нормализованные с exp=1 идут через одинаковый шаг. Нормализованные числа с exp=2 идут через удвоенный шаг, с exp=3 -- через учетверённый, и так далее. Иллюстрация распределения чисел: Иллюстрация распределения

Арифметические операции

  • Умножение числа на степень двойки. Достаточно прибавить/вычесть из показателя степени (учитывая переполнения).
  • Умножение двух чисел. Достаточно сложить их показатели степени и перемножить мантиссы. При этом в мантиссе может также получиться число >= 2, тогда надо его нормализовать и прибавить 1 к показателю степени. Если мантисса результата не влезает в 23 бита, её надо округлить. Если хвост < 1/2 или > 1/2, то округляется вниз или вверх, соответственно. Если хвост в точности 1/2, то округлять всегда в одну сторону плохо, т.к. при большом количестве последовательных операций может накопиться существенная погрешность. Поэтому в этом случае округляется к ближайшему чётному (то есть, если предыдущий бит равен 0, то вниз, если 1 -- вверх). Пример:
  |23 бита|           |23 бита|
1,01.....1101111 -> 1,01.....11   // хвост < 1/2, округляем вниз
  |       |           |       |
1,01.....0110011 -> 1,01.....10   // хвост > 1/2, округляем вверх
  |       |           |       |
1,01.....0010000 -> 1,01.....00   // хвост = 1/2, округляем вниз
  |       |           |       |
1,01.....0110000 -> 1,01.....10   // хвост = 1/2, округляем вверх
  • Деление аналогично.
  • Сложение и вычитание. Привести оба числа к одинаковому показателю степени, выполнить операцию, привести к нормализованному или денормализованному виду и округлить по правилам выше, если потребуется.

Свойства арифметических операций

  • При корректных арифметических операциях получается либо число, либо бесконечность.

  • Сложение и умножение коммутативны

  • Ассоциативности нет. Из-за округления в процессе выполнения операций могут получиться разные результаты. Например, \((3.14 + 2^{100}) - 2^{100} = 0\), но \(3.14 + (2^{100} - 2^{100}) = 3.14\). Из-за этого, для сохранения точности выполнять операции стоит в определённом порядке. Например, если хотим сложить массив вещественных чисел в одно число, лучше всего делать это в порядке сортировки чисел по возрастанию модулей.

  • У конечных чисел есть обратный элемент по сложению.

  • Монотонность: \(a\geq b \implies a+c\geq b + c\), если нет переполнений и NaN-ов.

Вещественные числа в C

Типы и их особенности в C

В C есть типы float, double и long double. На нашей системе они имеют размер 4, 8 и 12 байт соответственно. В 64-битном формате exp занимает 11 бит, а frac -- 52. Некоторые гарантии на арифметику:

  • f = -(-f) -- верно всегда.
  • (d < 0) => (2d < 0) -- верно всегда, в том числе если получается -inf.
  • (d > f) => (-f < -d) -- верно всегда
  • d * d >= 0 -- верно всегда

Считая, что int также 32-битный, рассмотрим приведения типов:

  • float -> double: преобразуется точно.
  • double -> float: может потеряться точность или стать inf (если был большой по модулю показатель степени).
  • int -> double: преобразуется точно, поскольку влезает в мантиссу.
  • int -> float: будет округлён, если int большой по модулю и есть маленькие биты (не влезает в мантиссу).
  • float/double -> int: дробная часть будет отброшена. Не определено, если целая часть не влезает в int.

Работа с вещественными числами в C

Для наглядности далее будет полезно запускать такой код. Он выводит все части числа в удобном формате:

#include <stdio.h>
#include <math.h>

#define CHECK(exp) printf(#exp " == %d\n", (exp))

int main() {
	union {
		float f;
		unsigned u;
	} uf;
	while (scanf("%f", &uf.f) == 1) {
		printf("f (%%e) = %e\n", uf.f);
		printf("f (%%f) = %f\n", uf.f);
		printf("f (%%g) = %g\n", uf.f);
		printf("f (%%a) = %a\n", uf.f);
		printf("u = %x\n", uf.u);
		printf("sign = %u\n", uf.u >> 31);
		printf("exp = %u\n", (uf.u >> 23) & 0xff);
		printf("frac = %x\n", uf.u & 0x7fffff);
		CHECK(fpclassify(uf.f));
		CHECK(isnan(uf.f));
		CHECK(isfinite(uf.f));
		CHECK(isinf(uf.f));
		CHECK(isnormal(uf.f));
	}
}

Спецификаторы printf:

  • %f, %e, %g -- float/double в 10-ой системе счисления.
  • %a -- float/double в 16-ой СС. Мантисса и показатель степени (c учётом смещения) разделаются символом p. Например, 4.375 = 0x1.18p+2.

Функции для работы с вещественными числами:

  • int fpclassify(float/double) -- возвращает класс числа, то есть одно из следующих значений: FP_NAN, FP_INFINITE, FP_ZERO, FP_SUBNORMAL, FP_NORMAL.
  • int isnan(float/double) -- является ли число NaN.
  • int isfinite(float/double) -- является ли число не NaN и не бесконечностью.
  • int isinf(float/double) -- 1, если +inf, -1, если -inf.
  • int isnormal(float/double) -- является ли число нормализованным.

Чтобы использовать функции из math.h, необходимо компилировать программу с флагом -lm.

Инструкции для работы с вещественными числами

У процессора есть отдельные регистры для обработки нескольких значений за одну инструкцию и, соответственно, отдельные инструкции для работы с этими регистрами. Есть 128-битные регистры XMM0-XMM31. В них можно поместить, например, 2 double, 4 float, 4 int, 8 short и т.д. Также есть 256-битные регистры YMM0-YMM31, являющиеся расширениями соответствующих XMM (по аналогии с AX->RAX). Аналогично, есть их 512-битные расширения, называемые ZMM0-ZMM31.

Эти регистры исторически добавлялись в следующем порядке: XMM->YMM->ZMM. Инструкции для работы с YMM называются SSE, а для работы с ZMM -- AVX. Мы на курсе будем работать только с SSE.

SSE инструкции:

  • MOVAPD xmm1/m128 xmm2 -- положить два double, записанные в xmm1 (или в памяти) в xmm2. Если переклыдавем из памяти, она должна быть выровнена на 16 байт.
  • MOVUPD xmm1/m128 xmm2 -- то же самое, только нет требования к выравниванию. Работает дольше. К счастью, и gcc при входе в функцию стек выравнивает на 16 байт, и *alloc выделяет память, выровненную на 16 байт, поэтому всегда можем использовать MOVAPD.
  • ADDPD xmm1/m128 xmm2 -- прибавить два double из xmm1 или из памяти к xmm2 поэлементно.
  • MOVSS e*x/m32 xmm2 -- загружает в младшие 32 бита xmm2.
  • HADDPD xmm1/m128 xmm2 -- выполняет "горизонтальное" сложение в двух числах отдельно и записывает в результат эти результаты подряд: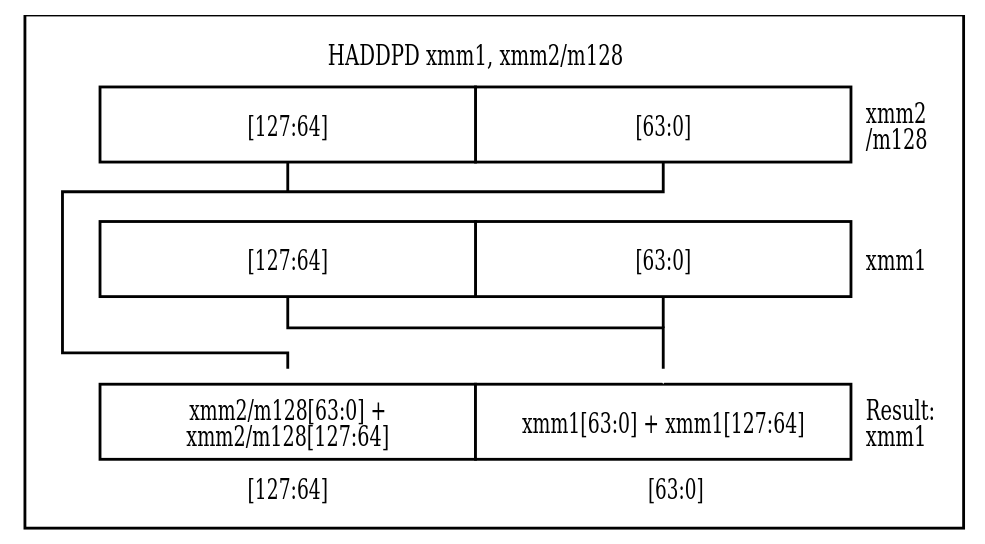 HADDPD example

Все регистры XMM caller-saved (не надо сохранять внутри функции).

Как gcc компилирует работу с вещественными числами.

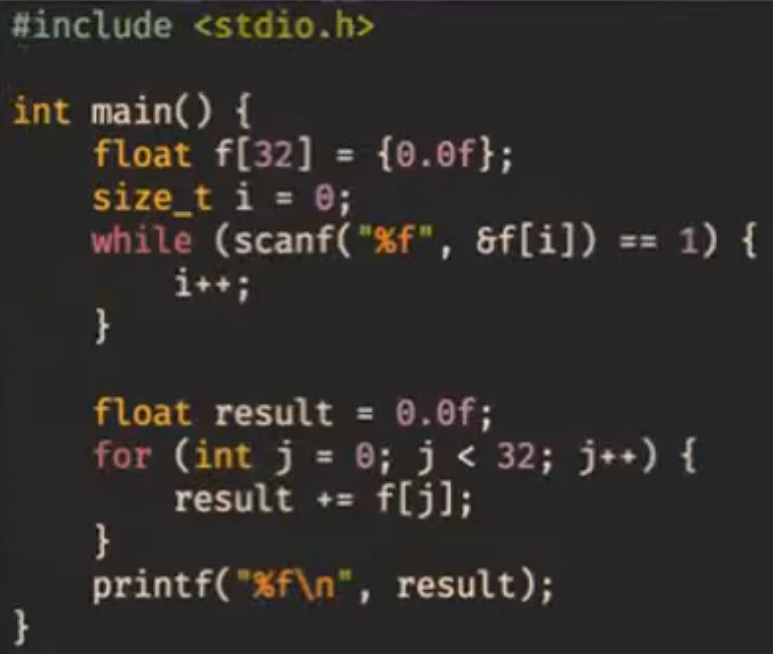
Посмотрим, как следующая программа выглядит при компиляции с разными оптимизациями: C_float_example

  1. Компилируем эту программу gcc без флагов оптимизации и в 32-битном режиме. Поскольку на 32-битной архитектуре мы не можем гарантировать, что процессор поддерживает SSE, то компилятор генерирует инструкции из устаревшего набора x87 (для сопроцессора). Мы с таким работать не хотим, поэтому идём дальше.
  2. Соберём без -m32 (то есть для 64-битной архитектуры). Получились SSE-инструкции, но пока что работающие с float-ми по-одиночке. 64bit build O0
  3. Соберём с O3 и -mavx -ftree-vertorize. Так мы скажем компилятору, что доступны инструкции AVX, и чтобы он векторизовал операции. Но он почему-то всё равно не векторизует :(

Чтобы печатать float-ы через printf на 32-битной архитектуре, используются инструкции x87. А на 64-битной параметры типа float и double в printf передаются через регистры xmm. Подробнее не будем изучать.

Алгоритм Кэхэна

Чтобы сложить много вещественных чисел более точно, можно использовать такой алгоритм, учитывающий ошибку округления:

function KahanSum(input)
    var sum = 0.0                 // Prepare the accumulator.
    var c = 0.0                   // A running compensation for lost low-order bits.

    for i = 1 to input.length do  // The array input has elements indexed input[1] to input[input.length].
        var y = input[i] - c      // c is zero the first time around.
        var t = sum + y           // Alas, sum is big, y small, so low-order digits of y are lost.
        c = (t - sum) - y         // (t - sum) cancels the high-order part of y; subtracting y recovers negative (low part of y)
        sum = t                   // Algebraically, c should always be zero. Beware overly-aggressive optimizing compilers!
    next i                        // Next time around, the lost low part will be added to y in a fresh attempt.

    return sum

Идея в том, что отдельно считаются неточная сумма больших по модулю чисел (переменная sum) и компенсация для накопленной ошибки округления (переменная c).